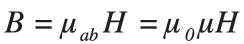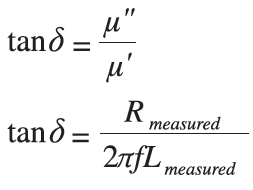Ферритовые материалы TDK
В начале 30-х годов два профессора Токийского Технологического университета Йогоро Като и Такеши Такеи изобрели ферриты – магнитные материалы, представляющие собой смесь оксида железа Fe2O3 с оксидами других металлов (таких как Fe, Mn, Zn, Ni, Mg, Co, Cu) и обладающие ферромагнетизмом. Вскоре после этого, в 1935 году, и была основана компания TDK, которая впервые поставила производство магнитомягких ферритовых материалов для использования в промышленности и технике.
Первым продуктом TDK на рынке стали «оксидные кольца» (рис. 1) для изготовления трансформаторов и катушек индуктивности. Уже с начала своей истории развития приоритетом для TDK стали инновационные разработки в области улучшения свойств ферритовых материалов и поиск новых областей их применения в электронной технике.

Основные электромагнитные параметры ферритовых материалов
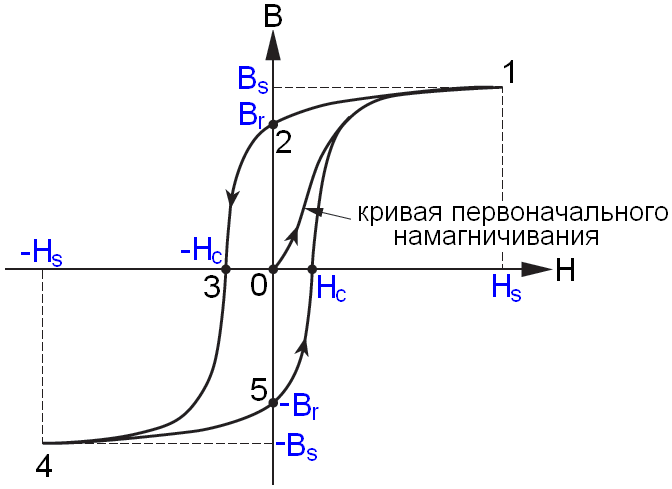
Рассмотрим фундаментальное свойство ферритового материала - гистерезис (рис. 2). Пусть изначально имеется полностью размагниченный феррит - точка 0. По мере увеличения прикладываемого внешнего магнитного поля Н, идёт процесс намагничивания феррита до индукции насыщения Bs по кривой 0-1, так называемой кривой первоначального намагничивания. Далее убирая внешнее поле, т.е. снижая напряженность поля до нуля, феррит размагничивается по кривой 1-2, сохраняя в отсутствии внешнего поля магнитный момент, характеризующийся величиной остаточной магнитной индукции Br. Магнитная индукция обращается в нуль лишь под действием внешнего поля Нс, имеющего направление, противоположное полю, вызвавшему намагничивание. Напряженность Нс называется коэрцитивной силой. Продолжая прикладывать магнитное поле в противоположном направлении, магнитная индукция выходит снова на насыщения Bs. При действии на феррит переменного магнитного поля индукция будет изменяться согласно кривой 1-2-3-4-5-1, которая носит название петли гистерезиса.
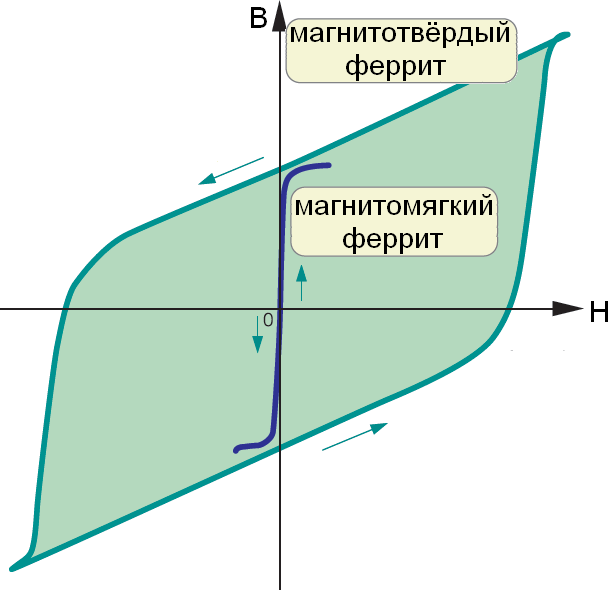
Условно в зависимости от ширины петли гистерезиса, ферритовые материалы можно поделить на магнитотвёрдые и магнитомягкие (рис. 3).
- Магнитотвёрдые ферриты обладают большими значениями коэрцитивной силы Нс и остаточной намагниченности Br. Намагничиваются до насыщения и перемагничиваются в сравнительно сильных магнитных полях, характеризуются широкой петлёй гистерезиса.
- К магнитомягким ферритам относят материалы с малой коэрцитивной силой Нс и высокой магнитной проницаемостью µ. Они обладают способностью намагничиваться до насыщения в слабых магнитных полях, характеризуются узкой петлёй гистерезиса.
Одним из важных параметров ферритовых материалов является магнитная проницаемость. Связь магнитной проницаемости µ, напряженности магнитного поля Н и магнитной индукции В выражается следующей формулой:
µab - абсолютная магнитная проницаемость
µo - магнитная проницаемость вакуума (4π х 10-7 Гн/м)
µ - относительная магнитная проницаемость.
Абсолютная магнитная проницаемость µab данного материала равна произведению относительной магнитной проницаемости µ на магнитную проницаемость вакуума µo. Относительная магнитная проницаемость среды показывает во сколько раз индукция магнитного поля в данной среде отличается от индукции этого же поля в вакууме. Относительная магнитная проницаемость среды является безразмерной величиной.
Как видно из вышеприведенной формулы, при приложении внешнего магнитного поля Н магнитная индукция внутри феррита В усиливается тем больше, чем больше относительная магнитная проницаемость µ.
В связи с нелинейной зависимостью B = f(H) проницаемость µ не является величиной постоянной. На рис. 4 приведена характерная зависимость магнитной проницаемости µ ферритового материала от напряженности магнитного поля Н. Здесь же представлена кривая первоначального намагничивания В(Н).
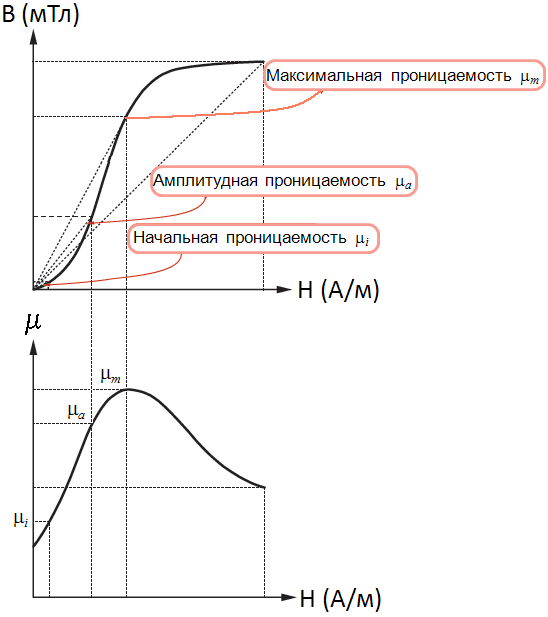
Начальная магнитная проницаемость µi определяется тангенсом угла наклона касательной в точке, где напряженность поля H → 0, к основной кривой намагничивания. Для описания поведения магнитного материала в переменном магнитном поле вводится амплитудная проницаемость µa, определяемая как тангенс угла наклона прямой, проведенной из начала координат в точку кривой намагничивания. Максимальное значение проницаемости µm достигается при приближении к области насыщения кривой намагничивания, после чего при дальнейшем увеличении напряженности магнитного поля H, начинается ее падение.
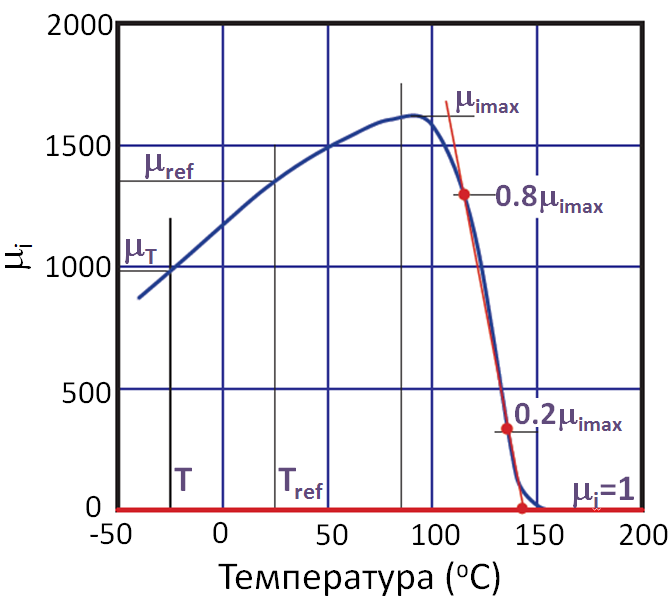
Величина магнитной проницаемости ферритов также изменяется с температурой (рис. 5), как правило, увеличивается по мере роста температуры и после достижения локального максимума при определённой температуре, проницаемость начинает уменьшаться до проницаемости вакуума μ=1. Температура, при которой магнитные свойства феррита исчезают, называется температурой Кюри. Эта температура определяется следующим образом: на графике зависимости магнитной проницаемости от температуры откладывается 2 точки 0.2 µimax и 0.8 µimax (20% и 80% от максимального значения начальной магнитной проницаемости, соответственно), проводится прямая через указанные две точки. Пересечение этой прямой с прямой µi = 1 , параллельной температурной оси, позволяет определить значение температуры Кюри.
Характер зависимости магнитной проницаемости от температуры зависит от свойств ферритового материала. Чтобы использовать феррит в широком температурном диапазоне, он должен иметь устойчивые электромагнитные характеристики, в частности с небольшим изменением магнитной проницаемости при изменении температуры. В качестве показателя изменения проницаемости от температуры вводят температурный коэффициент αµ проницаемости и относительный температурный коэффициент αF проницаемости:
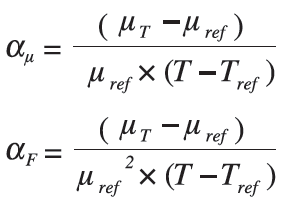
µref - магнитная проницаемость при референсной температуре Тref
µT - магнитная проницаемость при температуре ТТ
В качестве референсной температуры Тref рекомендуется брать 25 °С. Температура Т принадлежит тому температурному диапазону, в котором планируется использовать ферритовый материал (обычно это -40 °С, -25 °С, + 5 °С, + 55 °C, + 85 °C).
Связь между относительной магнитной проницаемостью µ и индуктивностью L выражается следующей формулой:
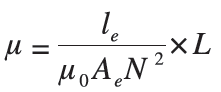
Ae - эффективная площадь поперечного сечения (м2)
le - эффективная длина магнитной силовой линии (м)
µо - магнитная проницаемость вакуума (4π х 10-7 Гн/м)
N - число витков.
Исходя из этой формулы видно, например, что нельзя допускать, чтобы дроссель работал с заходом в область насыщения, так как в этой области начинает резко падать проницаемость сердечника, а следовательно, индуктивность дросселя в этой области существенно уменьшится.
Для учёта характера изменения магнитного поля со временем вводится комплексная магнитная проницаемость, чтобы описать влияние среды на сдвиг фазы вектора магнитной индукции B по отношению к вектору напряженности магнитного поля H. Переменное магнитное поле индуцирует вихревые ЭДС в окружающих проводниках, при это возникают вихревые токи (токи Фуко), являющиеся источником потерь из-за омического сопротивления проводников.
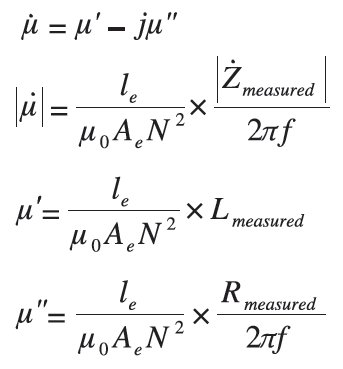
f - частота переменного магнитного поля(Гц)
Zmeasured - импеданс (Ω)
Lmeasured - индуктивность (Гн)
Rmeasured - сопротивление (Ω)
Как видно из представленных формул, µ' – это вещественная часть, обозначающая индуктивную компоненту, а µ'' – это мнимая часть, обозначающая резистивную компоненту.
Вещественная составляющая магнитной проницаемости µ' определяет величину запаса магнитной энергии в магнитном веществе, возвращаемого при размагничивании, мнимая часть µ'' определяет величину необратимых потерь на вихревые токи, перемагничивание (гистерезис), поглощение в веществе. Характеризуя потери, часто пользуются понятием тангенса угла магнитных потерь tanδ вещества. Это безразмерная величина, равная тангенсу угла между напряженностью магнитного поля Н и магнитной индукцией В, представляющих собой синусоидальные функции времени. Тангенс угла можно представить в следующем виде:
Угол δ называют углом потерь, поскольку для синусоидальных величин В и Н магнитные потери Р=π ƒ Вm Hm sinδ (где Вm и Hm - амплитудные величины) пропорциональны синусу этого угла, а для малых углов - самому углу.
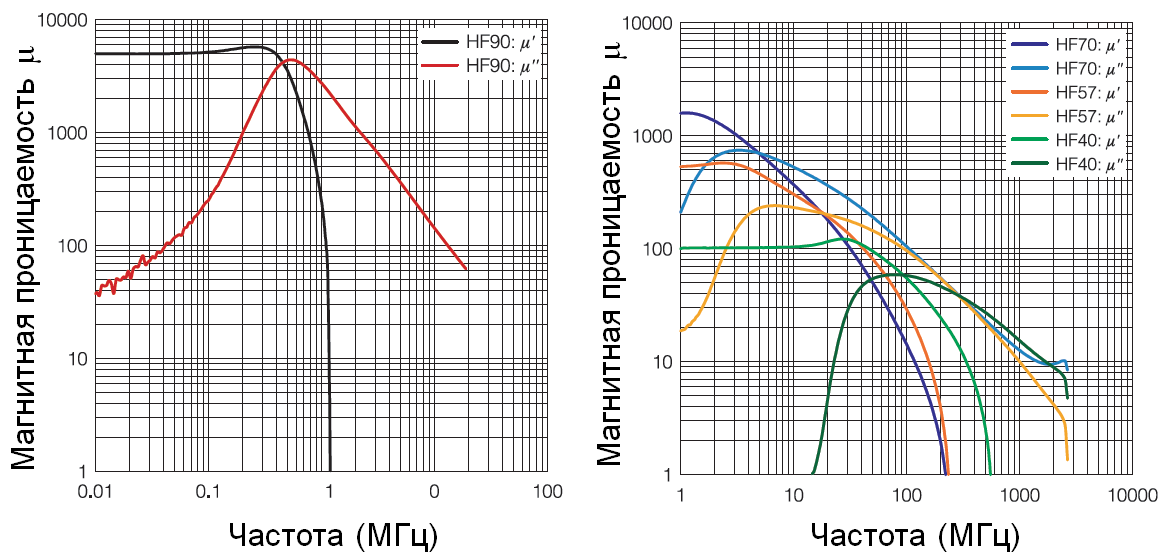
Важнейшей характеристикой магнитных материалов является зависимость комплексной магнитной проницаемости от частоты электромагнитного поля (дисперсия проницаемости). На рис. 5 в качестве примера приведены магнитные спектры (зависимости действительной части комплексной магнитной проницаемости от частоты) ряда никель-цинковых ферритов производства фирмы TDK, имеющих различную начальную магнитную проницаемость в диапазоне от 1 до 10000 МГц. Общим для всех спектров является существование области частот, где значение µ' остается постоянным. При более высоких частотах магнитная индукция В не успевает следовать за изменением магнитного поля Н, вызывая фазовый сдвиг. Из-за этого действительная часть проницаемости µ' (индуктивная компонента) довольно быстро падает до очень малых значений, а мнимая часть µ'' (резистивная компонента) начинает увеличиваться, и, следовательно, магнитные потери возрастают. Существует некоторое ограничивающее значение магнитной проницаемости в высокочастотной области, называемое пределом Сноека (на рис. 6 обозначен красной линией). Предел Сноека ограничивает частотный диапазон, допустимый для использования ферритового материала.
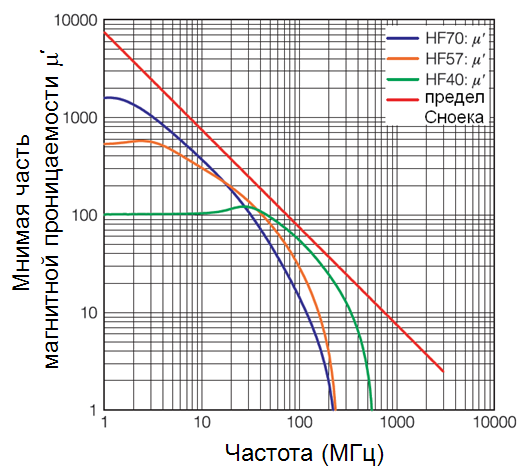
Видно, что в материалах (µi(HF70)=1500 > µi(HF57)=600 > µi(HF40)=120) с более высоким значением µi снижение действительной части магнитной проницаемости начинается в области более низких частот.
Кроме того, материалы (Bs(HF70)=280 мТл < Bs(HF57)=400 мТл < Bs(HF40)=410 мТл) с более высокой индукцией насыщения имеют более высокую граничную частоту, где они пригодны для использования.
Марганец-цинковые Mn-Zn и никель-цинковые Ni-Zn ферриты
Наибольшее распространение среди магнитомягких ферритовых материалов получили марганец-цинковые Mn-Zn и никель-цинковые Ni-Zn ферриты (рис. 7). Разнообразие марок Mn-Zn и Ni-Zn-ферритов определяется, главным образом, соотношением главных компонентов, наличием легирующих присадок и режимами синтеза.
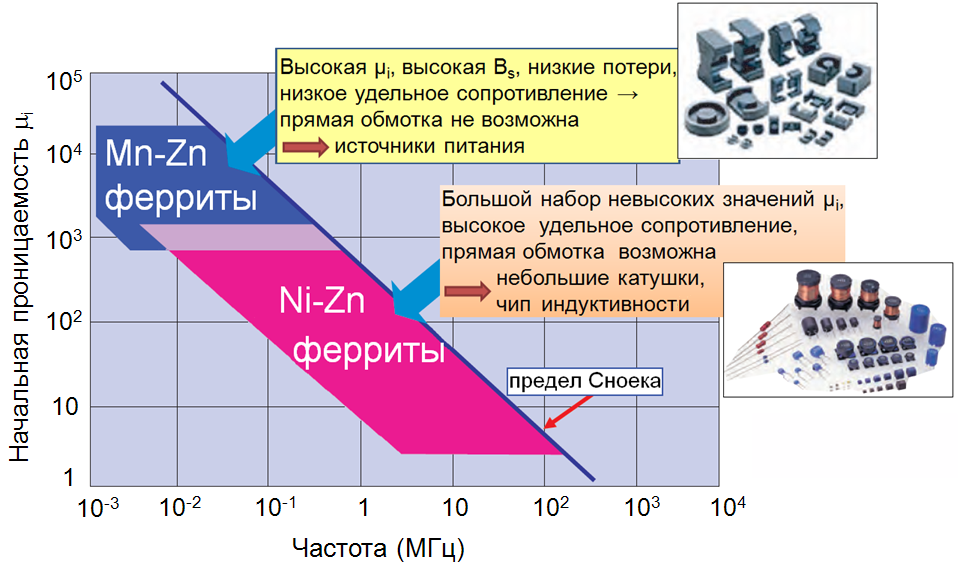
Отличительными особенностями Mn-Zn ферритов являются высокие значения начальной магнитной проницаемости μi и магнитной индукции насыщения Вs, при этом магнитные потери низкие. Недостатком является небольшое удельное сопротивление, что затрудняет их использовать при высоких частотах. Прямая обмотка не возможна, а значит, необходимо вводить изоляционный корпус, что приводит к увеличению массы и габаритов. Предел Сноека, показывает, что верхняя граница рабочей области частот ограничена 1 МГц и менее. Основное применение Mn-Zn ферритов - синфазные дроссели в линиях источников питания.
По сравнению с Mn-Zn ферритами, Ni-Zn ферриты имеют невысокие значения начальной проницаемости μi, и магнитной индукции насыщения Вs, высокие магнитные потери, однако удельное сопротивление высокое, поэтому прямая обмотка сердечника возможна. Ni-Zn ферриты используются для изготовления маленьких катушек индуктивности и чип индуктивностей, помехоподавляющих бусин и фильтров, помещенных в корпус.
Стоит отметить, что Mn-Zn ферриты обладают меньшей зависимостью магнитной проницаемости от напряженности магнитного поля по сравнению с никель-цинковыми. Ширина петли гистерезиса у них меньше ввиду меньших значений остаточной индукции и коэрцитивной силы при достаточно высоких значениях индукции. Особенностью марганцево-цинковых ферритов является более высокое значение температуры Кюри к по сравнению с никель-цинковыми ферритами и меньшие значения температурного коэффициента магнитной проницаемости.
В таблице 1 представлены характеристики ферритовых материалов TDK, используемых для кабелей круглого сечения (в том числе бусин), плоских кабелей и коннекторов.
| Название материала | HF90 | HF70 | HF57 | HF40 | HF30 |
|---|---|---|---|---|---|
| Материал | Mn-Zn | Ni-Zn | Ni-Zn | Ni-Zn | Ni-Zn |
| Начальная проницаемость μi | 5000 | 1500 | 600 | 120 | 45 |
| Относительный температурный коэффициент αi(x10-6/°С) | 1∼3 | 3∼5 | 8∼18 | 5∼15 | |
| Температура Кюри Tc°С | > 180 | > 100 | > 180 | > 250 | > 300 |
| Магнитная индукция насыщения Bs(мT) | 480 | 280 | 400 | 410 | 320 |
| Удельное сопротивление ρ(Ω⋅м) | 0.3 | 105 | 105 | 105 | 105 |
| Плотность db(x103кг/м3) | 4.8 | 5.0 | 5.0 | 5.0 | 5.0 |
| Рабочая область частот ν (МГц) | ∼1 | ∼500 | ∼500 | ∼600 | ∼1000 |
Рис. 8 демонстрирует зависимости вещественной и мнимой частей магнитной проницаемости от частоты для материалов, указанных в таблице 1. Обращает внимание то, что мнимая часть магнитной проницаемости μ˝ достигает максимального значения на частоте, на которой вещественная часть магнитной проницаемости μ' снижается примерно на половину по сравнению со значением начальной магнитной проницаемости. Сноек в 1948 г. объяснил такую взаимосвязь существованием ферромагнитного резонанса в поле магнитной анизотропии.
Характеристики ферритовых Mn-Zn материалов, используемых для изготовления синфазных дросселей, представлены в таблице 2.
| Название материала | HS52 | HS72 | HS10 |
|---|---|---|---|
| Материал | Mn-Zn | Mn-Zn | Mn-Zn |
| Начальная проницаемость μi | 5500 | 7500 | 1000 |
| Температура Кюри Tc°С | > 130 | > 130 | > 120 |
| Магнитная индукция насыщения Bs(мT) | 410 | 410 | 380 |
| Удельное сопротивление ρ(Ω⋅м) | 1 | 0.2 | 0.2 |
| Плотность db(x103кг/м3) | 4.9 | 4.9 | 4.9 |
| Рабочая область частот ν (МГц) | ∼1 | ∼500 | ∼500 |
Ферриты нашли широкое применение в качестве фильтров, используемых как на сигнальных проводах для ослабления внешних помех, так и на проводах питания для уменьшения создаваемых ими помех.
Один из возможных способов помехоподавления - использование ферритового сердечника как индуктивного элемента. Для обычного ферритового кольца (бусины) провод либо продевается через кольцо, образуя одновитковую катушку индуктивности, либо образует многовитковую тороидальную обмотку, что увеличивает индуктивность и, соответственно, эффективность помехоподавления. Также используются разборные фильтры в корпусе на защёлках. В этом случае (при использовании ферритового сердечника как индуктивного элемента) важно использовать ферритовый материал в области частот, где вещественная часть начальной магнитной проницаемости μ' имеет высокое значение, чтобы значение индуктивности было наибольшим.
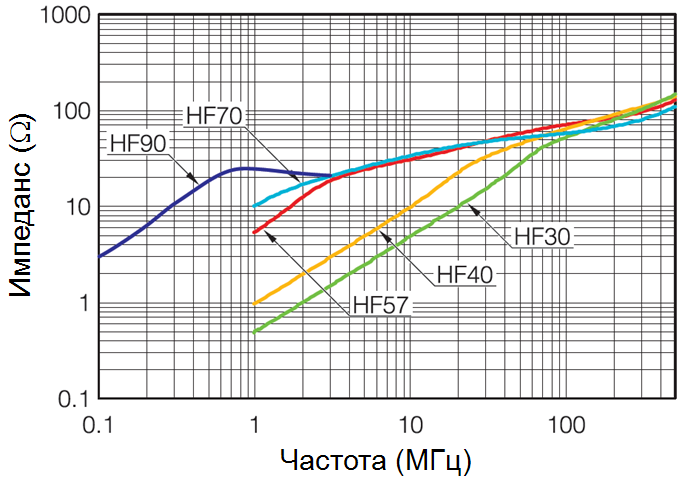
Часто ферритовые сердечники используются для отсечения помех посредством импеданса. В этом случае важно правильно подобрать не только материал феррита, но и конфигурацию сердечника, количество витков, чтобы получить импеданс достаточной величины для достижения помехоподавления в требуемой области частот. В этом случае помехи отражаются, но не исчезают. На рис. 9 представлены зависимости импеданса от частоты для кольца типоразмера 20х10х20 из ферритовых материалов HF90, HF70, HF57, HF40, HF30.
Для ферритового вещества импеданс носит комплексный характер Z=(R,X). Его активная составляющая R связана, в первую очередь, с проводимостью. Реактивная компонента X определяется емкостными свойствами.
На рис. 10 (слева) представлены графики частотных характеристик импеданса, а также его активной и реактивной составляющих для бусины типоразмера 6.4х5х3.2 из Ni-Zn феррита HF70. Частота, при которой реактивная X и активная R компоненты импеданса совпадают, называется ферромагнитной резонансной частотой, и зависит от материала феррита. Для Ni-Zn феррита HF70 резонансная частота равна 6 Мгц. Ниже этой частоты, полное сопротивление определено в основном индуктивной составляющей Х. В диапазоне 6 МГц - 100 МГц, ситуация меняется, теперь активная составляющая импеданса R доминирует, именно в этой области помехи могут быть поглощены (без отражения).
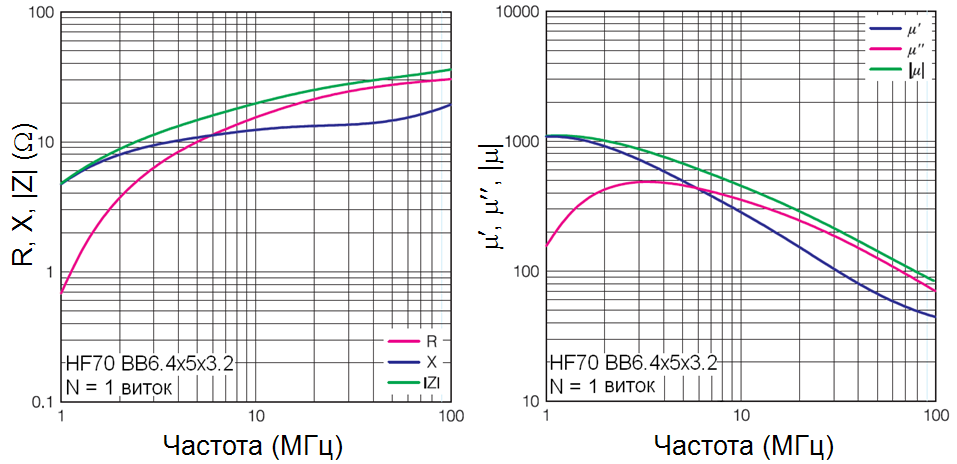
На рис. 10 (справа) представлены зависимости модуля комплексной магнитной проницаемости, его действительной и мнимой частей от частоты, рассчитанные из частотных характеристик импеданса. Как видно из представленных графиков, имеются взаимосвязи между μ' и L(X), μ’’ и R, |μ| и |Z|, соответственно. Ниже резонансной частоты, начальная магнитная проницаемость определена в основном вещественной составляющей μ', а выше - мнимая составляющая проницаемости μ’’ доминирует.